Mini-Project #2
|

|
This page describes mini-project #2 for Computer
Networks.
Markov modeling is an important tool for performance evaluation of
computer and communications systems. In this mini-project the student
will solve four Markov modeling problems. The student will submit
a solution for each problem carefully showing their work. This
mini-project is to be completed individually with help only to be
given by the instructor (that is,students may not "work together").
Problem #1: For the CTMC below do the following.
- Write and then solve as three equations in three unknowns the Q matrix.
- Use uniformization to convert the Q matrix to a P matrix. Give the P matrix
and then solve it as three equations in three unknowns
- Solve the P matrix using the power (iterative) method. Hint: You can use
iter.c found on the
Christensen
Tools page and show a screenshot of the execution.

Problem #2: You are given a system or component (for example, a
transceiver) with three states, BUSY, IDLE, and SLEEP (corresponding to the
system or component being powered-on and busy, powered-on and idle, and
sleeping, respectively). Let the power draw of each state be as follows:
- BUSY = 1 W
- IDLE = 0.8 W
- SLEEP = 0.1 W
Periodically, once per minute the system transitions between states
(including to the same state) with a known probability as given below. What
is the average power draw of this system or component? Write the state equations
and solve them both directly and iteratively (e.g., using
iter.c found on the
Christensen
tools page)
- BUSY to BUSY with probability 0.50, BUSY to IDLE with probability 0.25, and
BUSY to SLEEP with probability 0.25
- IDLE to IDLE with probability 0.25, IDLE to BUSY with probability 0.50, and
IDLE to SLEEP with probability 0.25.
- SLEEP to SLEEP with probability 0.25 and SLEEP to BUSY with probability
0.75.
Problem #3: Consider an M/M/2/4 queue (a queue with two service centers
and a buffer with capacity of two customers) with arrival rate 1.0
customers/second and service rate of 1.0 customers/second for each service
center. Answer the following questions:
a) Sketch the continuous time Markov chain for this queue.
b) Solve the Markov chain for steady state probabilities and mean number in
the system.
Problem #4: You have invented a new method of routing packets end-to-end
to minimize packet delay. You think that your method is better (that is, mean
packet delay is less) than existing methods. To evaluate your method you have
conducted experiments on a network test bed sending packets from multiple
sources to a given destination. You have measurement results for the existing
routing method and your new routing method (which you inserted into the network
test bed routers). Your measurement results are:
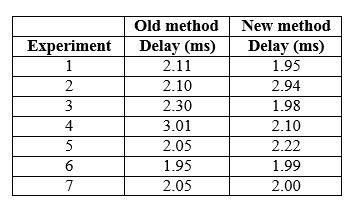
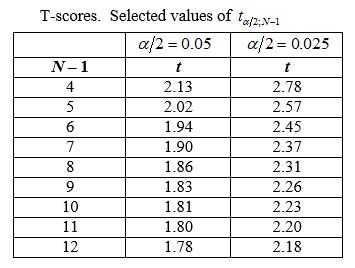
You believe that your experiments are representative of the real Internet. Is
your method better? Should it be deployed in the Internet? Below is a T-score
table that may be helpful to your argument.
Grading
Grading is as follows (each problem is 25% of the overall grade):
- Problem #1
- Q matrix and its direct solutions -- 33%
- P matrix and its direct solutions -- 33%
- Iterative solution -- 33%
- Problem #2
- P matrix and its direct solutions -- 50%
- Iterative solution -- 50%
- Problem #3
- Part (a) -- 50%
- Part (b) -- 50%
- Problem #4
- T-Test steps -- 33%
- T-Test calculations -- 33%
- Conclusion (is it better) -- 25%
- Conclusion (should it be deployed) -- 9%
|
Last update on August 26, 2014
|




