ISCI

The ability to see around corners would be profoundly useful in numerous fields, from helping see past partial blockages in medical settings to enabling surveillance while remaining undetected. Such systems could leverage existing sensing hardware to gather information about hidden pedestrians, vehicles, or other potential obstacles and allow autonomous vehicles to plan safer trajectories through intersections or into occluded spaces.

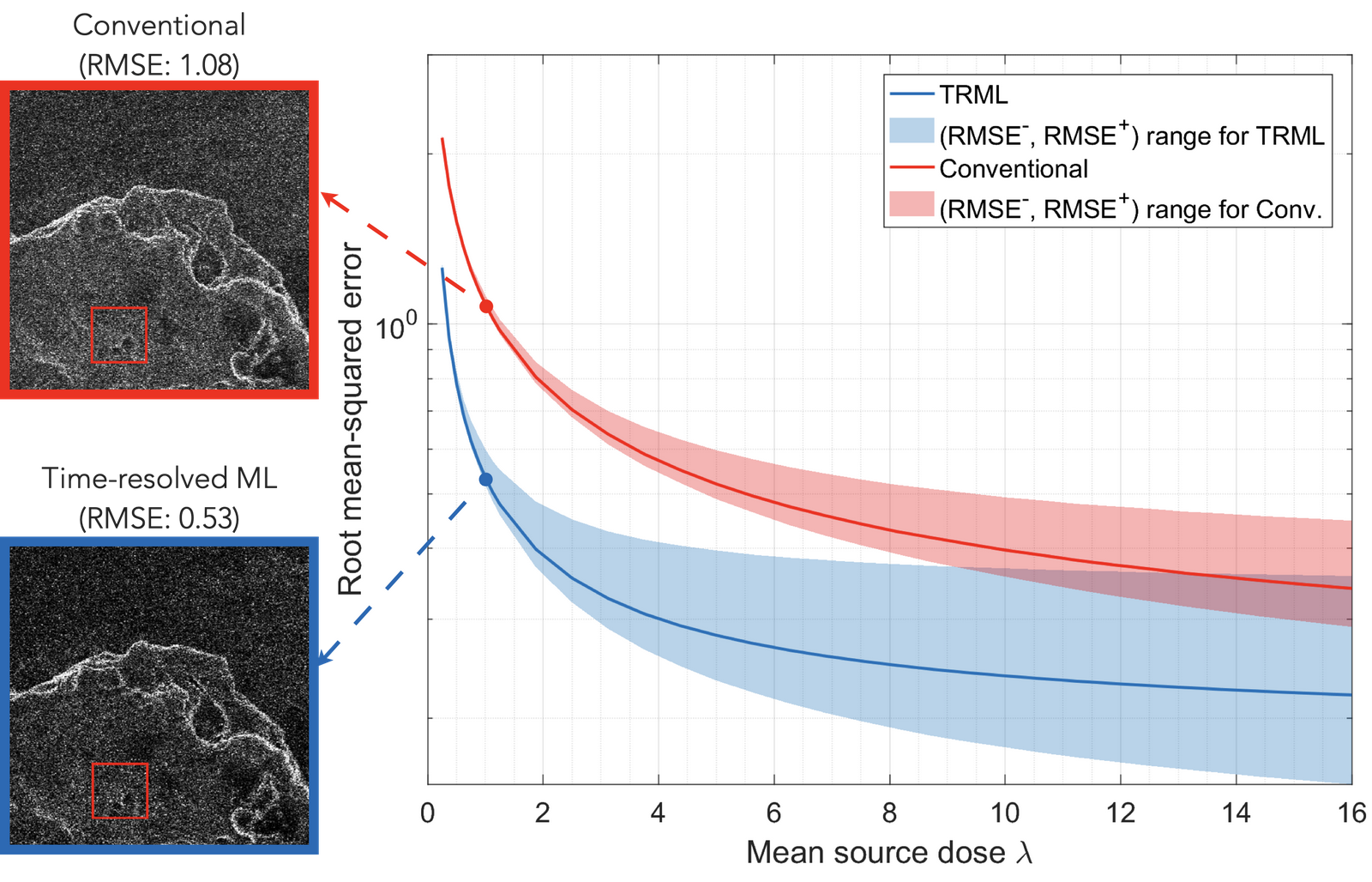
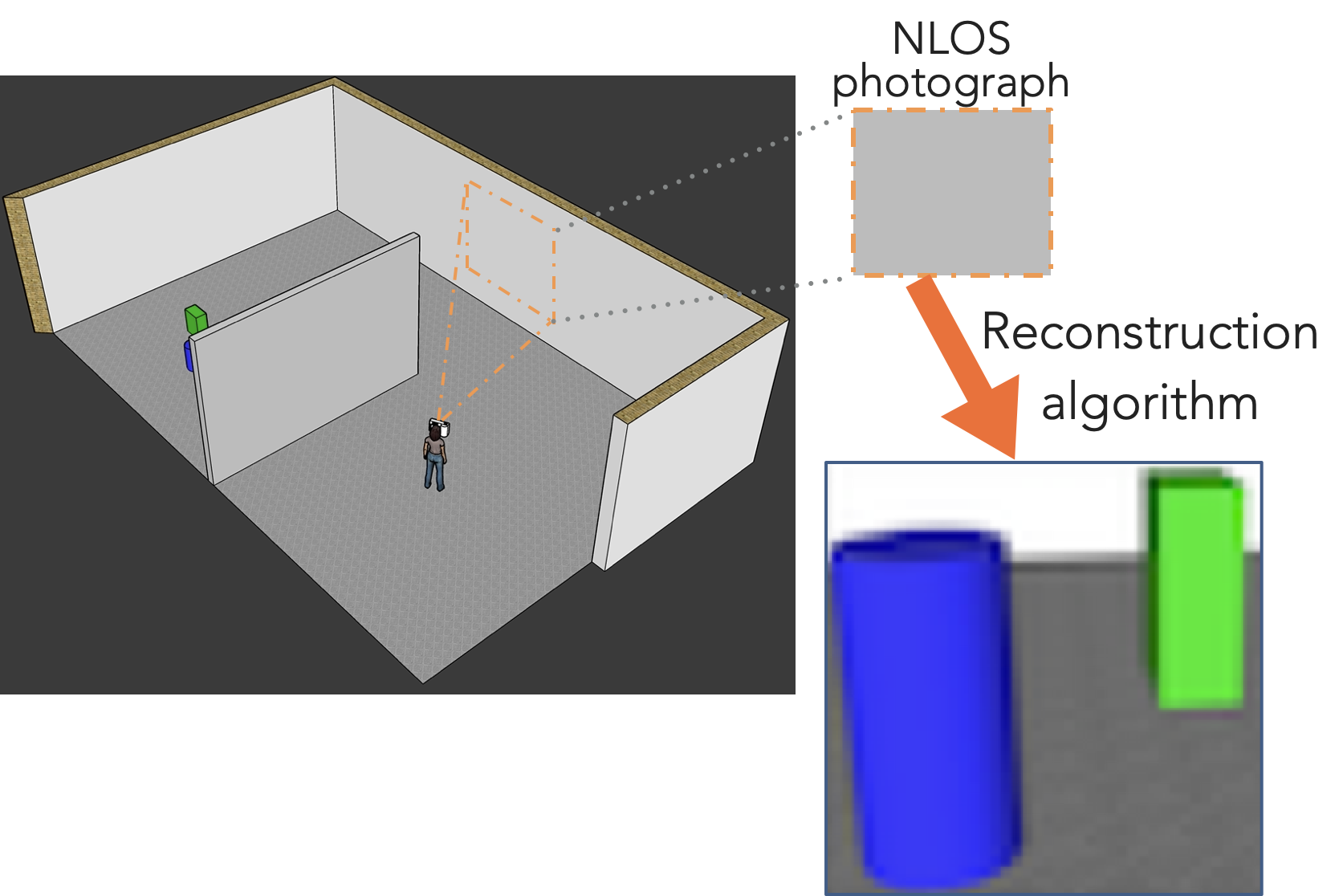
Computational periscopy with an ordinary digital camera. Our work demonstrates how subtle variations of penumbrae in a single, brief snapshot of a diffuse surface using a consumer digital camera can enable non-line-of-sight scene estimates.

Manuscripts:
More details can be found in our  manuscript  and  online supplementary materials .

Code availability: Data and code to reproduce results are  available on Github .

Press coverage:

• Nature:  Shadows used to peer around corners , and  How an ordinary camera can see around corners
• The Guardian:  Program allows ordinary digital camera to see around corners
• Economist:  A camera that can see around corners .

Focussed Ion Beam Microscopy.

Helium ion microscopes (HIM), scanning electron microscopes (SEM), and other focussed-ion beam (FIB) microscopes enable imaging with unprecedented spatial resolution by raster scanning the intended sample's surface with a focused beam of particles, Unfortunately, that process of imaging often causes damage to the sample and necessitates keeping the radiation dose low. However, low dose yields noisier images.

Source shot noise mitigation and low dose imaging.  Our analyses demonstrate that low-dose measurements have the most Fisher information per incident ion. This inspires a time-resolved acquisition approach (realized by obtaining multiple extremely low dose acquisitions, instead of a single high dose acquisition) and a tailored algorithm that together yields unprecedented improvements in imaging accuracy when compared to the conventional method. 

Papers:  Ultramicroscopy ,  IEEE Trans. on Comp. Imaging .

Source estimation and field reconstruction.

Numerous biological and physical phenomena can be accurately described by partial differential equations. For example, the diffusion equation models thermal variations, disease epidemic dynamics, and the dispersion of biochemical substances. Poisson's equation relates the measured electrical potentials and the current dipoles in neuronal source activity monitoring using electroencephalographic (EEG) signals; and the wave equation models propagation of acoustic fields in acoustic tomography. We aim to recover the unknown sources and reconstruct the entire field, from few spatiotemporal samples obtained using a network of sensors.

Papers: 

Estimating Localized Sources of Diffusion Fields using Spatiotemporal Sensor Measurements.

A sampling framework for physics-driven inverse source problems.